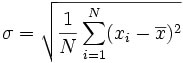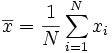
Do you understand the meaning of this equation?
The mean, ![]() ,
of a set of measurements is defined as the sum of the measurement values,
divided by the number of measurements. The
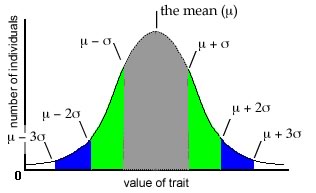
normal distribution is also characterized by a number known as the standard
deviation or σ (sigma).
,
of a set of measurements is defined as the sum of the measurement values,
divided by the number of measurements. The
normal distribution is also characterized by a number known as the standard
deviation or σ (sigma).